Blog
Stray Light Analysis (Part 3)
Modelling stray light both correctly and efficiently requires making the most suitable choice from the available scatter models and setting up the system such that enough of the scattered light makes it to the region of interest.
FRED’s impressive choice of scatter models and importance sampling options are vital to help you get the right results quickly. In this article, we’ll take a look at a simple case followed by a more complex multiple scatter model.

Figure 1. Scatter models can be set up with differing levels of scattering efficiency
Representing Surface Scatter
FRED’s surface scatter models generally fall into three categories, parameterized (i.e. mathematically modelled), tabulated (i.e. measured and optionally fitted data), and scripted - where you are free to write your own scattering function.
| Type | Model | Description |
|---|---|---|
| Tabulated | Tabular BSDF | Interpolated BSDF scatter data |
| Tabulated PSD | Interpolated BSDF from surface profile data | |
| Diffuse Polynomial | Fitted measured tabular data | |
| Diffuse Binomial | Fitted measured tabular data (Plane-symmetric) | |
| Parameterized | Lambertian | Idealized diffuse scatter |
| Harvey-Shack | Scatter from polished surface microroughness | |
| Extended Harvey-Shack | Harvey-Shack with additional angle dependence | |
| ABg | Scatter from polished surface microroughness | |
| Flat Black Paint | Diffuse reflectance based on Aeroglaze Z306 | |
| Surface Particle (Mie) | Scatter from small surface particulates | |
| K-Correlation | Microrough scatter as PSD | |
| Phong | Scatter that follows Cos^n relationship | |
| Scripted | Scripted | User-defined BASIC script |
| Extended Scripted | As above with support for polarization |
These scatter models can be chosen to apply in reflection and/or transmission and optionally remove the specular ray which can be necessary for truly diffuse surfaces.
Modeling Scatter Efficiently
Raytracing software handles scattering events by generating some number of random rays from the surface with powers calculated from the scattering definition. We’ll take a look at a simple example of a highly reflective Lambertian scattering surface where some distance above the scattering surface is an annulus that represents the entrance pupil of some other system the light is scattered into. For simplicity, a detector is placed behind this aperture, at which we wish to measure the number of scattered rays entering the annulus.

Figure 2. A highly reflective Lambertian surface-emitting into a hemisphere in the absence of importance sampling. Only 0.8% of scattered rays make it through the annulus to the detector.
Allowing rays to randomly be generated in all directions can sometimes be necessary but in a model such as the above where the aim is to measure the power scattered in a certain direction (towards our annulus), this is woefully inefficient. Only 8 of the1000 scatter rays that are generated make it to the region of interest.
The use of importance sampling remedies this problem by generating rays that go into a specific direction of interest and therefore generate more signal at our detector.
FRED supports six types of importance sampling
| Importance Sampling Type | Description |
|---|---|
| Scatter rays into given direction | Scatter into a user-defined cone angle centered around a specified direction |
| Scatter rays into the specular direction | Scatter into a user-defined cone angle centered around the specular ray |
| Scatter rays toward an entity | Scatter toward the bounding box of an entity (can be non rotationally symmetric) |
| Scatter rays toward a point | Scatter into a user-defined cone angle centered on a specific point in space |
| Scatter rays toward an ellipsoidal volume | Scatter towards an ellipse centered at a specific point (can be non rotationally symmetric) |
| Scatter rays through a closed curve | Scatter towards an existing user-defined curve (can be non rotationally symmetric) |
One approach to get rays to scatter towards the region of interest is to place a spherical target inside the aperture of the screen and direct the rays towards this. In FRED this can be done with either the options to scatter to a point or elliptical volume.

Figure 3. Zoomed in view of a sphere (ellipse) that represents the importance sampling target, the sphere is centered on the annular screen in front of the detector.
The FRED definitions for this setup are shown in figures 4 and 5.

Figure 4. The scatter properties and importance sampling (Direction Regions of Interest). Note that more than one scatter model and region of interest can be defined and active.

Figure 5. Definition of the spherical target. Each of the importance sampling types has further options to control the number of scattered rays and scatter ancestry cut-offs.
This definition is much more efficient than scattering into a hemisphere and all the rays go in the general direction of interest.

Figure 6. Scattering to a sphere is more efficient than no importance sampling but still not ideal as the circular annulus appears elliptical in shape when viewed from the scattering surface.
However, still only 462 of the 1000 scatter rays that were generated made it to the region of interest inside the annulus. Whilst this is a great increase from the 0.8% efficiency seen without importance sampling this result also demonstrates the limitations of using spherical targets to represent planar apertures at high angles of incidence.
In reality, the annulus representing the entrance pupil of the following optical system is compressed into the shape of an ellipse when viewed from the perspective of the scattering surface, and this cannot be adequately represented by a sphere.
In this case, the other importance sampling options FRED has to offer are advantageous. Perhaps the simplest and most efficient approach, in this case, is to use FRED’s option to scatter towards a curve, where that curve describes the opening of the annular surface.

Figure 7. Scatter to a (circular) curve located at the annulus. In this case, the 100% of the rays make it through the annulus to the detector.
Now all of the 1000 scattered rays generated make it to the region of interest, yielding an efficiency of 100%.
| Importance Sampling Used | Efficiency |
|---|---|
| None | ~0.8% |
| Scatter to Sphere | ~46% |
| Scatter to Curve | 100% |
The above comparison of importance sampling choices and ray efficiency clearly highlights the need to choose the importance sampling technique to be used.
Modelling Multiple Scatter Events to Multiple Targets
The prior examples all show one scatter model being used in conjunction with one importance sampling, and whilst this is fine in simple situations FRED is capable of hosting multiple scatter models and targets on the same surface, this means that it’s possible to stack scattering events in different ways including:
- Surfaces where reflected and transmitted scatter functions are different
- Surfaces that exhibit different scattering characteristics such as a polished surface that exhibits both microroughness (Harvey-Shack) and particulate contamination (Mie).
- Surfaces that preferentially scatter in multiple directions
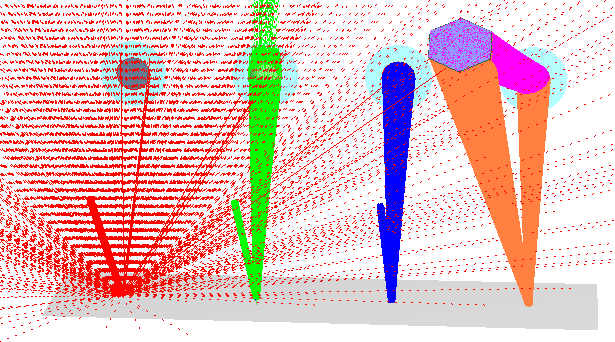
As a final example to demonstrate this we will add a secondary scattering surface which rescatters the light from the first scattering surface. To make this more complex still the secondary scattering surface will be a tilted hexagonal plane (something that cannot be well represented by a sphere). The raytrace shows the effects.

Figure 8. Example of secondary scattering from a tilted hexagonal plane. The secondary scattered rays are shown in purple.
In this simulation the first scattering surface has two active scatter models to represent both surface diffuse and particulate scatter, and two directions of interest - one to the annulus and the other to the hexagonal surface. The secondary scatter surface is set to scatter towards the annulus.

Figure 9. Application of multiple scatter models and scatter directions to the primary scattering surface
Note that FRED’s scatter UI also gives the ability to toggle models off and on as needed without losing the definitions.
Summary
FRED has thirteen scatter model options and six types of importance sampling to give you the widest choice in simulating the toughest scatter problems, such as those seen in Stray Light Analysis, with ease. FRED’s importance sampling options allow for highly efficient ray traces which reduce the number of rays needed and therefore calculation times.
