Blog


Exploring Temporal Pulse Propagation with FRED
Understanding and simulating temporal pulse propagation is crucial for applications involving nonlinear optical materials, laser ablation, and other high-precision tasks. In this blog post, we delve into how FRED software enables the design and simulation of pulse trains, with a focus on Gaussian pulse trains.
Introduction
Pulsed laser operation is essential for engaging nonlinear optical materials and exploring phenomena that occur in extremely short timeframes. The high peak power in a pulse is also vital for laser ablation. FRED software allows users to design and simulate desired pulse trains, providing a powerful tool for optical engineers and researchers.
Defining a Time-Limited Light Pulse
A time-limited light pulse can be created by summing weighted plane waves of varying light frequencies. The relationship between the pulse duration and its spectral distribution is governed by Fourier transform principles. This inverse relationship means that shorter pulses require a broader range of wavelengths.
The Fourier Transform Limit
The Fourier transform limit defines the relationship between pulse duration (Δt\Delta tΔt) and bandwidth (Δω\Delta \omegaΔω), stating that ΔωΔt≥0.5\Delta \omega \Delta t \geq 0.5ΔωΔt≥0.5. This principle underscores the necessity of a wide spectral range to create very short pulses.
Pulse Trains in FRED
Creating a practical light pulse often involves generating a repeating train of light pulses. By manipulating the spectral distribution, users can control the shape, width, and spacing of these pulses. The spacing between pulses, known as the Free Spectral Range (tFSRt_{FSR}tFSR), is determined by the frequency spacing Δω\Delta \omegaΔω.

Figure 1: Pulse train with Free Spectral Range spacing.
Example: Gaussian Pulse Train
A Gaussian pulse train is a common pulse shape due to its mathematical simplicity and practical relevance. In FRED, designing a Gaussian pulse train involves several steps:
For this example, the Gaussian pulse has a Full Width at Half Maximum (FWHM) of 10 ps and a central wavelength of 1064 nm, with a pulse spacing of 12.5 mm in a vacuum.

Figure 2: Temporal profile of Gaussian pulse.
The central frequency is derived from the central wavelength, and the frequency spacing is calculated based on the Free Spectral Range. The pulse spectrum is then obtained by taking the Fourier transform of the pulse.
Creating the Pulse in FRED
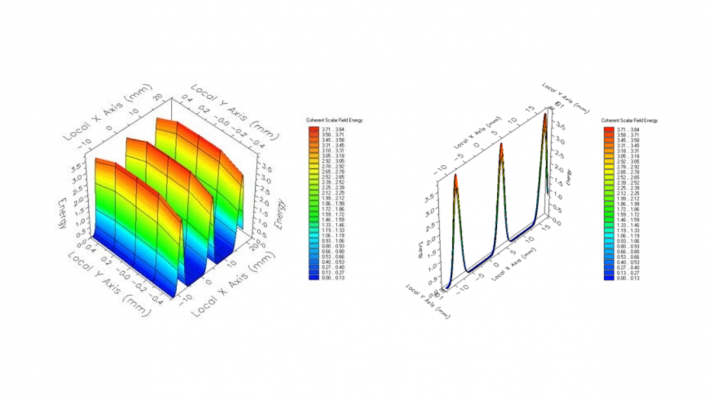
After determining the necessary frequencies and relative magnitudes, these are input into FRED. A detector with a length greater than 12.5 mm along the optical axis allows the pulses to be plotted in space. Although FRED typically adds different wavelength components incoherently, an embedded script can enforce coherent addition of each wavelength's field, generating the overall pulse profile on the detector.

Figure 3: Series of 3 Gaussian pulses measured along an axial detector from a coherently-added multi-spectral plane wave.
Conclusion
FRED software offers a robust platform for simulating temporal pulse propagation, enabling precise design and analysis of optical pulses. By following the outlined steps, users can create and manipulate pulse trains to suit various applications, from laser ablation to nonlinear optics.
____________________________________________________________________________________________________________________________________________________________________________________
This blog post was created based on the information provided by Photon Engineering, a partner of CBS Europe.