Blog


Mastering Spatial Filtering with FRED Software
Spatial filtering is a critical technique in laser optics, designed to enhance laser beam quality by removing unwanted noise and higher-order modes. This blog post delves into the advanced spatial filtering techniques using FRED software, focusing on the simulation of laser beam propagation through a spatial filter using Gaussian Beam Decomposition (GBD) and Gabor Decomposition. These methods ensure precise modeling of laser systems, enhancing the accuracy of optical designs.
Understanding Spatial Filters
A spatial filter typically consists of a pinhole aperture placed at the focal point of a lens system. It allows only the desired mode of the laser beam to pass through while blocking higher-order modes and noise. Properly modeling this process in FRED involves re-synthesizing the light field after it passes through the spatial filter, ensuring that the clipping effects at the aperture are accurately captured.
Gaussian Beamlet Model of Coherent Light
In FRED, coherent light is modeled using Gaussian Beam Decomposition (GBD), where the light field is divided into individual Gaussian beamlets. These beamlets propagate coherently, maintaining phase relationships, and are represented by a set of rays.
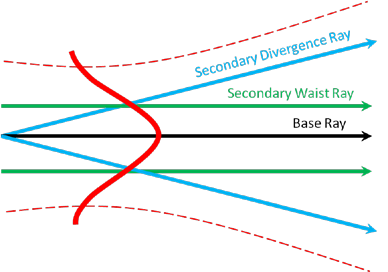
Figure 1: Complex ray representation of a Gaussian beamlet.
When laser light is focused through a spatial filter, most base rays will pass through the aperture, potentially neglecting the clipping effect. To address this, FRED allows for resampling of the light field within the aperture, generating a new set of rays for further propagation.
Applying Gabor Decomposition in FRED
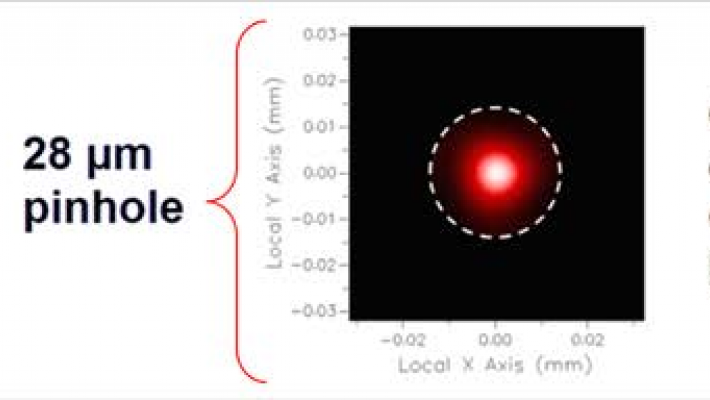
To demonstrate spatial filtering in FRED, consider a system where collimated HeNe laser light passes through a spatial filter. The filter diameter is calculated based on the lens focal length and beam diameter. A custom aperture element is created in FRED to simulate the spatial filter.
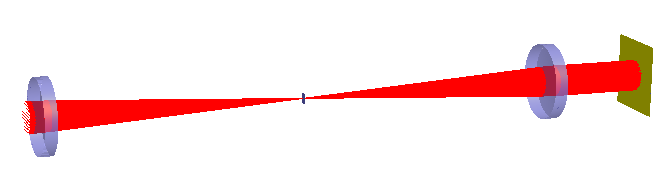
Figure 2: Spatial filtering of HeNe laser light.
After setting up the spatial filter, the light field at the spatial filter plane is clipped and resynthesized using Gabor Decomposition. This process ensures that the beam is accurately modeled, including the effects of clipping at the spatial filter.
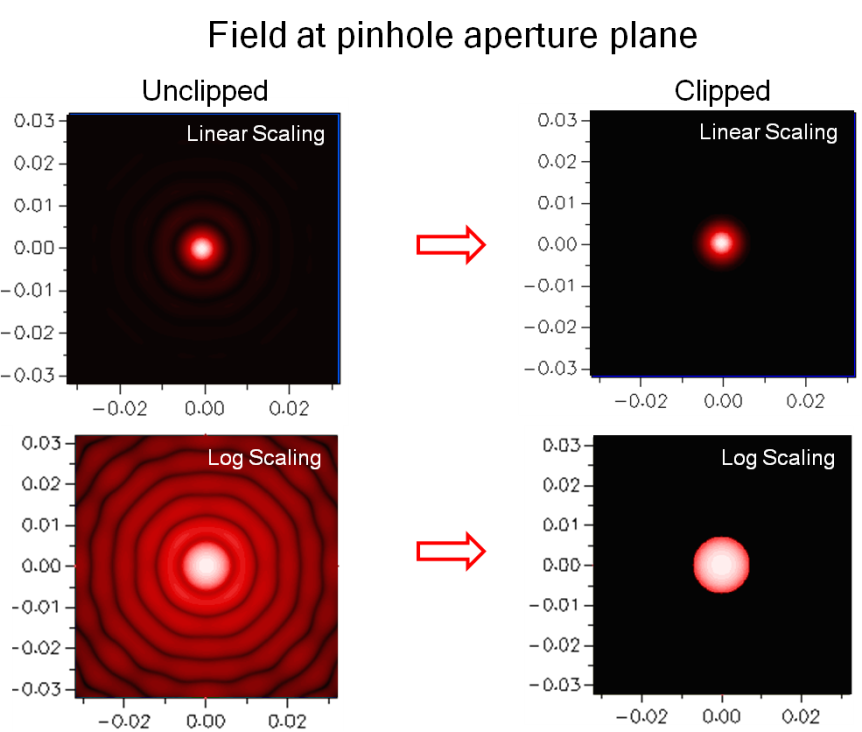
Figure 3: The result of clipping the light field within the spatial filter aperture.
Accurate Propagation Beyond the Spatial Filter
Finally, a new set of complex rays should be generated within the clipped region. This is accomplished using Gabor decomposition. In the graph, right-click and select Coherent Field Operations Synthesize Field. Check the output window to ensure that new rays have been created. Coherent field synthesis parameters are shown in Figure 4. Finally, select “Trace Existing” to model light propagation beyond the spatial filter. Figure 5 shows irradiance distribution beyond the collimating lens with field synthesis compared to a distribution that neglects spatial filter clipping. It is clear that field synthesis accurately models the reduced beam diameter and expected diffraction characteristics.
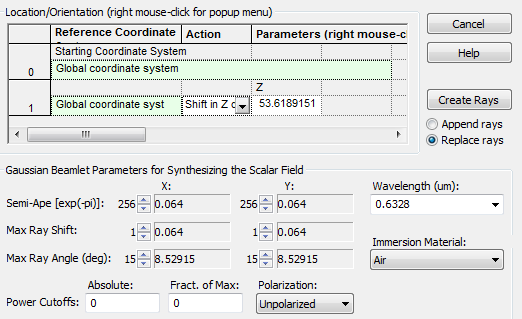
Figure 4. Coherent field synthesis parameters. Gabor decomposition is a directional synthesis that requires maximum beamlet semi-aperture. Maximum ray shift is set to 1 to ensure beam overlap. The diameter of the next optic determines the maximum ray angle. In this case, the collimating lens requires a maximum angle of at least 8°. For more information on Gabor decomposition, Photon Engineering’s Physical Optics Modeling short course is recommended.
The resulting beam is traced through the system once the light field is resynthesized within the spatial filter. The synthesis parameters ensure that the beam accurately reflects the reduced diameter and diffraction characteristics expected from the filtering process.
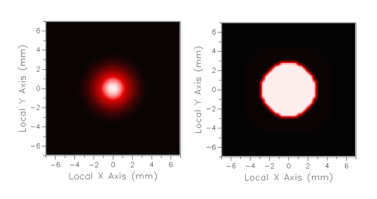
Figure 5: Irradiance distribution beyond the collimating lens. Left: With resynthesized field. Right: Without field synthesis, ignoring clipping effects.
Conclusion
FRED software’s advanced modeling capabilities, including GBD and Gabor Decomposition, provide the precision needed to accurately simulate spatial filtering in laser systems. This allows optical designers to predict and optimize beam quality in applications requiring stringent control over laser beam profiles.
_________________________________________________________________________________________________________________________________________________________________________________
This blog post was created based on the information provided by Photon Engineering, a partner of CBS Europe.